Metodos Cuantitativos 2: Valor Absoluto

Objetivos de Aprendizaje

Resolver una ecuación con valor absoluto.
Analizar soluciones a las ecuaciones con valor absoluto.
Graficar funciones con valor absoluto.
Resolver problemas del mundo real usando ecuaciones con valor absoluto.

Introducción

El valor absoluto de un número es su distancia desde cero en la recta numérica. Existen siempre dos números en la recta numérica que están a la misma distancia desde cero. Por ejemplo, los números 4 y -4 están ambos a una distancia de 4 unidades a partir de cero.

$\mid 4 \mid$ representa la distancia desde 4 a cero la cual es igual a 4.

$\mid -4 \mid$ representa la distancia desde -4 a cero la cual es igual a 4.

De hecho, para cualquier número real $x$ ,

$\mid x \mid =x$ Si $x$ no es negativa (eso es, incluyendo $x = 0.$ )

$\mid x \mid = -x$ Si $x$ es negativa.

El valor absoluto no tiene efecto en un número positivo pero cambia un número negativo en su inverso positivo.

Ejemplo 1

Evaluar los siguientes valores absolutos.

a) $\mid 25 \mid$

b) $\mid -120 \mid$

c) $\mid -3 \mid$

d) $\mid 55 \mid$

e) $\mid -\frac{5}{4} \mid$

Solución:

a) $\mid 25 \mid \ =25$ Ya que 25 es un número positivo, el valor absoluto no lo cambia.

b) $\mid -120 \mid \ =120$ Ya que -120 es un número negativo, el valor absoluto lo hace positivo.

c) $\mid -3 \mid \ =3$ Ya que -3 es un número negativo, el valor absoluto lo hace positivo.

d) $\mid 55 \mid \ =55$ Ya que 55 es un número positivo, el valor absoluto no lo cambia.

e) $\mid -\frac{5}{4} \mid \ =\frac{5}{4}$ Ya que es un número negativo, el valor absoluto lo hace positivo.

El valor absoluto es muy útil para encontrar la distancia entre dos punto en la recta numérica. La distancia entre dos puntos $a$ y $b$ en la recta numérica es $\mid a-b \mid$ o $\mid b-a\mid$ .

Por ejemplo, la distancia desde 3 a -1 en la recta numérica $\mid 3 - (-1) \mid = \mid 4 \mid =4$ .

Podríamos también haber encontrado la distancia sustrayendo en orden inverso, $\mid -1-3 \mid = \mid -4 \mid =4$ .

Esto tiene sentido porque la distancia es la misma si partes de 3 a -1 o desde -1 a 3.

Ejemplo 2

Encontrar la distancia entre los siguientes puntos en la recta numérica.

a) 6 y 15

b) -5 y 8

c) -3 y -12

Soluciones

La distancia es el valor absoluto de la diferencia entre los dos puntos.

a) Distancia = $\mid 6 -15 \mid = \mid -9 \mid = 9$

b) Distancia = $\mid -5 - 8 \mid = \mid -13\mid = 13$

c) Distancia = $\mid -3 - (-12) \mid = \mid 9 \mid = 9$

Recuerda: Cuando calculamos el cambio en $x$ y el cambio en $y$ como parte del cálculo de la pendiente, Estos valores fueron positivos o negativos, dependiendo de la dirección del movimiento. En esta discusión, “distancia” significa únicamente una distancia positiva.

Resolver una Ecuación con Valor Absoluto

Ahora queremos resolver ecuaciones que involucran valores absolutos. Considera la siguiente ecuación.

$\mid x \mid =8$

Esto significa que la distancia desde el número $x$ a cero es 8. Existen dos números posibles que satisfacen esta condición 8 y -8.

Cuando resolvemos ecuaciones con valor absoluto siempre considera dos posibilidades.

La expresión dentro del símbolo del valor absoluto no es negativa.
La expresión dentro del símbolo de valor absoluto es negativa.

Entonces resolvemos cada ecuación separadamente.

Ejemplo 3

Resolver las siguientes ecuaciones con valor absoluto.

a) $\mid 3 \mid =3$

b) $\mid 10 \mid = 10$

Solución

a) Existen dos posibilidades $x=3$ y $x=-3$ .

b) Existen dos posibilidades $x=10$ y $x=-10$ .

Analizar las Soluciones para Ecuaciones con Valor Absoluto

Ejemplo 4

Resolver la ecuación e interpretar las respuestas.

Solución

Consideramos dos posibilidades. La expresión dentro del símbolo de valor absoluto es o no negativa. Luego resolvemos cada ecuación separadamente.

$x-4=5 & & & & x-4=-5\\x=9 & & \text{y} & & x=-1$

Respuesta $x=9$ y $x=-1$ .

Ecuación $\mid x -4 \mid =5$ puede ser interpretada como “que números en la recta numérica están 5 unidades alejados del número 4?” Si dibujamos la recta numérica observamos que hay dos posibilidades 9 y -1.

Ejemplo 5

Resolver la ecuación $\mid x +3 \mid =2$ e interpretar la respuesta.

Solución

Resolver las dos ecuaciones.

$x + 3 & = 2 & & & & x + 3 = -2\\x & = -1 & & \text{y} & & \qquad x=5$

Respuesta $x=-5$ y $x=-1$ .

La ecuación $\mid x +3 \mid =2$ puede reescribirse como $\mid x - (-3)\mid =2$ . Podemos interpretar esto como “qué números en la recta numérica están 2 unidades alejados de -3?” Existen dos posibilidades -5 y -1.

Ejemplo 6

Resolver la ecuación $\mid 2x-7 \mid =6$ e interpretar las respuestas.

Solución

Resolver las dos ecuaciones.

$2x -7 & = -6 & & & & 2x -7 = 6\\2x & = 13 & & \text{y} & & \qquad 2x = 1\\x & = \frac{13} {2} & & & & \qquad \ \ x = \frac{1} {2}$

Respuesta $x=\frac{13} {2}$ y $x=\frac{1} {2}$

La interpretación de este problema es clara si la ecuación $\mid 2x-7 \mid =6$ fue dividida por 2 en ambos lados. Obtenemos $\mid x -\frac{7}{2}\mid =3$ . La pregunta es “Qué números en la recta numérica están 3 unidades alejados de $\frac{7}{2}$ ?” Existen dos posibilidades $\frac{13}{2}$ y $\frac{1}{2}$ .

Graficar Funciones con Valor Absoluto

Tú aprenderás ahora como graficar funciones con valor absoluto. Considera la función:

$y=\mid x -1 \mid$

Vamos a graficar esta función haciendo una tabla de valores.

$x$	$y=\mid x -1\mid$
$-2$	$y=\mid -2-1\mid = \mid -3 \mid =3$
-1	$y=\mid -1-1\mid = \mid -2 \mid =2$
0	$y=\mid 0-1\mid = \mid -1 \mid =1$
1	$y=\mid 1-1\mid = \mid 0 \mid =0$
2	$y=\mid 2-1\mid = \mid 1 \mid =1$
3	$y=\mid 3-1\mid = \mid 2 \mid =2$
4	$y=\mid 4-1\mid = \mid 3 \mid =3$

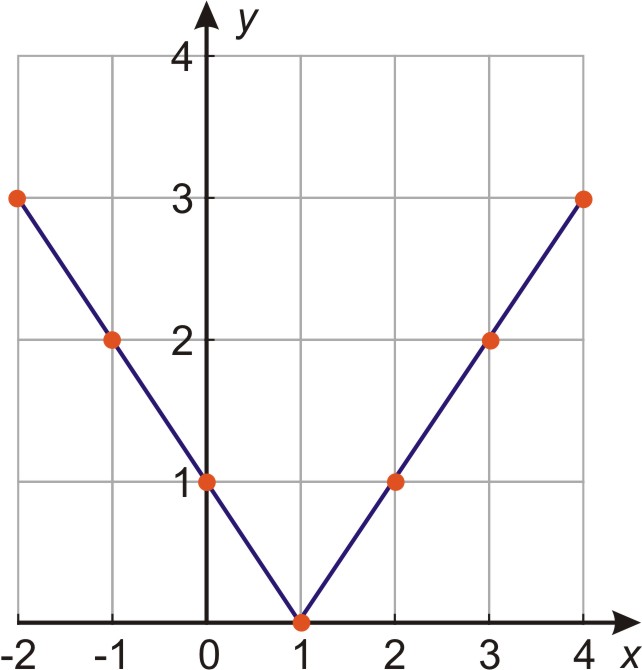
Tú puedes ver que el gráfico de una función con valor absoluto tiene la forma de una gran “V”. Consiste en dos rayos de líneas (o segmentos de lineas), uno con pendiente positiva y uno con pendiente negativa unidos por el vértice ocúspide.

Observamos en secciones previas que para resolver una ecuación con valor absoluto necesitamos considerar dos opciones.

La expresión dentro del valor absoluto no es negativa.
La expresión dentro del valor absoluto es negativa.

El gráfico de $y= \mid x -1\mid$ es una combinación de dos gráficos.

Opción 1

$y=x-1$

Cuando $x-1 \geq 0$

Opción 2

$y=-(x-1)$ o $y=-x+1$

Cuando $x-1 <0$

Ambos son gráficos de líneas rectas.

Las dos líneas rectas se encuentran en el vértice. Encontramos el vértice estableciendo la expresión dentro del valor absoluto igual a cero.

$x-1=0$ o $x=1$

Siempre podemos graficar una función con valor absoluto usando una tabla de valores. Sin embargo usamos gneralmente un procedimiento simple.

Paso 1 Encontrar el vértice del gráfico estableciendo la expresión dentro del valor absoluto igual a cero y resolver para $x$ .

Step 2 Hacer una tabla de valores que incluyan el vértice, un valor más pequeño que el vértice y un valor más grande que el vértice. Calcular los valores de $y$ usando la ecuación de la función.

Paso 3 Dibujar los puntos y conectarlos con dos líneas rectas que se encuentren en el vértice.

Ejemplo 7

Graficar la función con valor absoluto: $y=\mid x+5\mid$ .

Solución

Paso 1 Encontrar el vértice $x+5=0$ o $x=-5$ .

Step 2 Hacer una tabla de valores.

$x$	$y=\mid x+5\mid$
$-8$	$y=\mid -8+5 \mid = \mid -3 \mid =3$
-5	$y=\mid -5+5 \mid =\mid 0 \mid =0$
-2	$y= \mid -2+5\mid = \mid 3 \mid =3$

Paso 3 Colocar los puntos y Dibujar dos líneas rectas que se encuentren en el vértice.

Ejemplo 8

Graficar la función con valor absoluto $y=\mid 3x -12 \mid$ .

Solución

Paso 1 Encontrar el vértice $3x- 12 = 0$ entonces $x=4$ es el vértice.

Paso 2 Elaborar una tabla de valores:

$x$	$y=\mid 3x-12\mid$
0	$y=\mid 3(0)-12 \mid = \mid -12\mid =12$
4	$y=\mid 3(4)-12\mid = \mid 0 \mid =0$
8	$y=\mid 3(8)-12 \mid = \mid 12 \mid =12$

Paso 3 Dibujar los puntos y dibujar dos líneas rectas que se encuentren en el vértice.

Resolver Problemas del Mundo Real Usando Ecuaciones con Valor Absoluto

Ejemplo 9

Una compañia empaqueta granos de cafe en bolsas herméticas. Cada bolsa debería pesar 16 onzas pero es difícil llenar cada bolsa con el peso exacto. Después de ser llenadas, cada bolsa es pesada y si hay más de 0.25 onzas de sobrepeso o de peso inferior, es vaciada y vuelta a empacar. Cuáles son las bolsas más ligeras o pesadas aceptables?

Solución

Paso 1

Sabemos que cada bolsa debería pesar 16 onzas.

Una bolsa puede pesar 0.25 onzas más o menos que 16 onzas.

Necesitamos encontrar las bolsas con peso más liviano y aceptable y las más pesadas que son aceptables.

Dejar $x =$ peso de la bolsa de café en onzas.

Paso 2

La ecuación que describe este problema se escribe $\mid x -16 \mid 0.25$ .

Paso 3

Considerar las opciones positivas y negativas y resolver cada ecuación separadamente.

$x-16&=0.25 & & & & x-16 =-0.25\\& & \text{y} & & \\x&=16.25 & & & & \qquad \ x=15.75$

Respuesta La bolsa más liviana aceptable pesa 15.75 onzas y la más pesada 16.25 onzas.

Paso 4

Observamos que $16.25 - 16 = 0.25$ onzas y $16 - 15.75 = 0.25$ onzas. Las respuestas son 0.25 onzas más grande y 16 onzas menos.

La respuesta es correcta.

Resumen de la Lección

El valor absoluto de un número es su distancia a partir de cero en la recta numérica.

$\mid x \mid =x$ si $x$ no es negativo.

$\mid x \mid =-x$ si $x$ es negativo.

Una ecuación con valor absoluto en ella se separa en dos ecuaciones.

La expresión dentro del valor absoluto es positiva, entonces los símbolos del valor absoluto no hacen nada y pueden ser omitidos.
La expresión dentro del valor absoluto es negativa, entonces los símbolos del valor absoluto deben ser negados antes de remover signos.

Ejercicios de Repaso

Evaluar los Valores Absolutos.

$\mid 250 \mid$
$\mid -12 \mid$
$\mid -\frac{2}{5} \mid$
$\mid \frac{1}{10} \mid$

Encontrar la distancia entre los puntos.

12 y -11
5 y 22
-9 y -18
-2 and 3

Resolver las ecuaciones con valor absoluto e interpretar los resultados graficando las soluciones en la recta numérica.

$\mid x -5 \mid =10$
$\mid x +2 \mid =6$
$\mid 5x-2 \mid =3$
$\mid 4x-1 \mid =19$

Graficar las funciones con valor absoluto.

$y =\mid x +3 \mid$
$y = \mid x -6 \mid$
$y = \mid 4x+2 \mid$
$y = \mid \frac{x}{3}-4\mid$
Una compañía manufactura reglas. Sus reglas de 12- pulgadas pasan controles de calidad si están dentro de la longitud ideal $\frac{1}{32}$ pulgadas. Cuál es la regla mas larga y la más corta que puede salir de la fábrica?