Este es un espacio en el cual podemos interactuar y brindarnos ayuda unos a otros
lunes, 30 de junio de 2014
Ejercicios Ecuaciones Cuadraticas
Compañeros como se dio a conocer hoy terminamos con las funciones
cuadraticas acontinuacion dejo una pequeña lista de ejercicios a
realizar para fortalecer lo visto en clase
3) Hallen, si es que existen, las raíces reales de las siguientes
funciones:
a) f(x) = (x-3)2 – 9 b) g(x) = 4x2
– 5x
c) h(x) = – x2 – 4 d)
j(x) = x2 + 3x + 2
e) k(x) = –4x2 + 4x – 1
4) Grafiquen las siguientes funciones. Para ello, determinen previamente
las raíces reales, las coordenadas del vértice, la ecuación del eje de simetría
y el punto de intersección con el eje de las ordenadas (y).
p(x) = x2 - 2x - 8 q(x)
= - x2 + 6x - 9
r(x) = (2x - 1)(x + 2,5) s(x)
= -0,5(x + 1)2 – 1,5
t(x) = - x2 - x - 2
5) resolver
a) 3x – x2 + 0,1= 0 b)
x2 + 4 = 0 c) -1/9+2x – 9x2 = 0 d) 3x2 -1/2 = 0
6) Expresen en forma factorizada las siguientes funciones cuadráticas:
f(x) = x2 + x g(x)
= - x2 + 1 h(x)
= x2 + 6 x – 27
j(x) = -2 x2 - 7 x – 3 k(x) = - x2 + 12 x –
36 p(x) = 4 x2 – 1
7) Las
siguientes funciones cuadráticas están escritas en forma canónica. Exprésenlas
en forma factorizada:
f(x) = 2(x - 1)2 – 2 g(x) = 3(x + 1)2 –
12 h(x) = - x2 + 2
j(x) = 4(x
- 2)2 – 1 k(x)
= - 5(x + 4)2 q(x)
= 9(x + 1)2 – 4
8) Escriban cada una de las
siguientes funciones cuadráticas en los otros dos tipos de expresiones:
f(x) = 6
(x - 1)(x+9) g(x)
= 5 (x - 4)2 - 125
h(x) = - 3
x2 + 8x + 3 j(x)
= -4x2
jueves, 26 de junio de 2014
Unidad II Funciones Cuadraticas
Aquí un poco de teoría sobre las funciones cuadráticas:
Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:
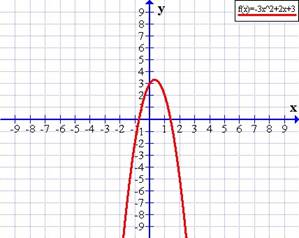
Si a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x2 + 2x + 3
Además, cuanto mayor sea |a| (el valor absoluto de a), más cerrada es la parábola.
Puntos de corte en el eje de las abscisas (Raíces o soluciones) (eje de las X)
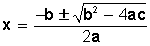
Observar que la parábola siempre cortará al eje de las ordenadas (Y), pero como ya vimos más arriba al eje de abscisas (X) puede que no lo corte, lo corte en dos puntos o solamente en uno.
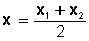
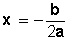
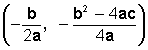
Función cuadrática |
Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:
f(x) = ax2 + bx + c
donde a, b y c (llamados términos) son números reales cualesquiera y a es distinto de cero (puede ser mayor o menor que cero, pero no igual que cero). El valor de b y de c sí puede ser cero.
En la ecuación cuadrática cada uno de sus términos tiene un nombre.
Así,
ax2 es el término cuadrático
bx es el término lineal
c es el término independiente
Cuando estudiamos la ecuación de segundo grado o cuadrática vimos que si la ecuación tiene todos los términos se dice que es un ecuación completa, si a la ecuación le falta el término lineal o el independiente se dice que la ecuación es incompleta.
Representación gráfica de una función cuadrática
Si pudiésemos representar en una gráfica "todos" los puntos [x,f(x)] de una función cuadrática, obtendríamos siempre una curva llamada parábola.
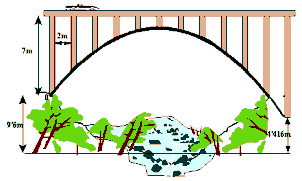 |
| Parábola del puente, una función cuadrática. |
Como contrapartida, diremos que una parábola es la representación gráfica de una función cuadrática.
Dicha parábola tendrá algunas características o elementos bien definidos dependiendo de los valores de la ecuación que la generan.
Estas características o elementos son:
Orientación o concavidad (ramas o brazos)
Puntos de corte con el eje de abscisas (raíces)
Punto de corte con el eje de ordenadas
Eje de simetría
Vértice
Orientación o concavidad
Una primera característica es la orientación o concavidad de la parábola. Hablamos de parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de parábola convexa si sus ramas o brazos se orientan hacia abajo.
Esta distinta orientación está definida por el valor (el signo) que tenga el término cuadrático (la ax2):
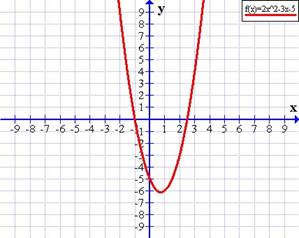
Si a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x2 − 3x − 5

Si a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x2 + 2x + 3

Además, cuanto mayor sea |a| (el valor absoluto de a), más cerrada es la parábola.
Puntos de corte en el eje de las abscisas (Raíces o soluciones) (eje de las X)
Otra característica o elemento fundamental para graficar una función cuadrática la da el valor o los valores que adquiera x, los cuales deben calcularse.
Ahora, para calcular las raíces (soluciones) de cualquier función cuadrática calculamos
f (x) = 0.
Esto significa que las raíces (soluciones) de una función cuadrática son aquellos valores de x para los cuales la expresión vale 0; es decir, los valores de x tales que y = 0; que es lo mismo que f(x) = 0.
Entonces hacemos
ax² + bx +c = 0
Como la ecuación ax² + bx +c = 0 posee un término de segundo grado, otro de primer grado y un término constante, no podemos aplicar las propiedades de las ecuaciones, entonces, para resolverla usamos la fórmula:
Entonces, las raíces o soluciones de la ecuación cuadrática nos indican los puntos de intersección de la parábola con el eje de las X (abscisas).
Respecto a esta intersección, se pueden dar tres casos:
Que corte al eje X en dos puntos distintos
Que corte al eje X en un solo punto (es tangente al eje x)
Que no corte al eje X
Esta característica se puede determinar analizando el discriminante, ya visto en las ecuaciones cuadráticas.
Ver: PSU: Matemática;
Punto de corte en el eje de las ordenadas (eje de las Y)
En el eje de ordenadas (Y) la primera coordenada es cero, por lo que el punto de corte en el eje de las ordenadas lo marca el valor de c (0, c).
Veamos:
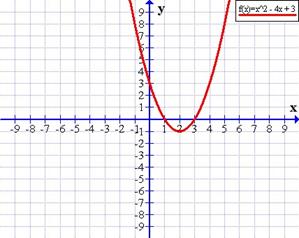
Representar la función f(x) = x² − 4x + 3

El eje de las ordenadas (Y) está cortado en +3
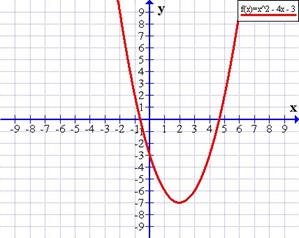
Representar la función f(x) = x² − 4x − 3

El eje de las ordenadas (Y) está cortado en −3
Observar que la parábola siempre cortará al eje de las ordenadas (Y), pero como ya vimos más arriba al eje de abscisas (X) puede que no lo corte, lo corte en dos puntos o solamente en uno.
Eje de simetría o simetría
Otra característica o elemento de la parábola es su eje de simetría.
El eje de simetría de una parábola es una recta vertical que divide simétricamente a la curva; es decir, intuitivamente la separa en dos partes congruentes. Se puede imaginar como un espejo que refleja la mitad de la parábola.
Su ecuación está dada por:
Donde x1 y x2 son las raíces de la ecuación de segundo grado en x, asociada a la parábola.
De aquí podemos establecer la ecuación del eje de simetría de la parábola:

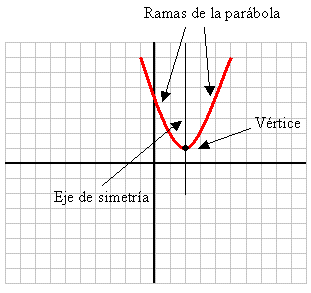
Vértice
Como podemos ver en gráfico precedente, el vértice de la parábola es el punto de corte (o punto de intersección) del eje de simetría con la parábola y tiene como coordenadas
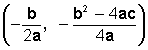
La abscisa de este punto corresponde al valor del eje de simetría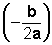 y la ordenada corresponde al valor máximo o mínimo de la función,
y la ordenada corresponde al valor máximo o mínimo de la función, 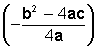 según sea la orientación de la parábola (recuerde el discriminante)
según sea la orientación de la parábola (recuerde el discriminante)
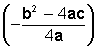 según sea la orientación de la parábola (recuerde el discriminante)
según sea la orientación de la parábola (recuerde el discriminante)Solucion alos Ejercicios
Soluciones a funciones lineales EJEMPLOS
1. f (x) = 5x + 13
m = la pendiente es 5
b = 13
2. f (x) = 24x
m = la pendiente es 24
la recta no cruza el eje de las y
3. f (x) = 3x + 2x +7
primero simplificamos:
f (x) = 5x +7
m = la pendiente es 5
b = 7
4. f (x) = -5x +12 -3
primero simplificamos:
f (x) = -5x +9
m = -5
b = 9
5. f (x) = 7x
m = 7
la recta no cruza el eje de las y
6. f (x) = 5x + 7 – 4
Primero simplificamos:
f (x) = 5x + 3
m = 5
b = 3
7. f (x) = 4x – 2x +3
Primero simplificamos:
f (x) = 2x +3
m = 2
b = 3
8. f (x) = x – 14
m = 1
b = -14
Espero que con estos ejemplos te haya quedado más claro el tema de funciones lineales, no olvides usar una tabla de valores para graficar tus funciones!
- See more at: http://matematicasmodernas.com/funciones-lineales-ejemplos/#sthash.E66ISfrW.dpuf
Ejercicios Funciones Lineales
Bueno compañero como el día de ayer terminamos con el tema de funciones lineales aquí una pequeña lista de ejercicios para practicar y entenderle mejor al tema
Encontrar la pendiente , los intercepto y graficar:
1. f (x) = 5x + 13
Encontrar la pendiente , los intercepto y graficar:
1. f (x) = 5x + 13
2. f (x) = 24x
3. f (x) = 3x + 2x +7
4. f (x) = -5x +12 -3
5. f (x) = 7x
6. f (x) = 5x + 7 – 4
7. f (x) = 4x – 2x +3
8. f (x) = x -14
sábado, 21 de junio de 2014
SEGUNDA UNIDAD
Relaciones y Funciones
"Los matemáticos no estudian los objetos, sino las relaciones
entre los objetos; por tanto les es indiferente reemplazar
estos objetos por otros, con tal que no cambien las relaciones".
Henri Poincaré.1.1 Coordenadas de un punto en el plano cartesiano.
Objetivos.
a) Determinar un sistema de ejes coordenados.
b) Localizar puntos en el plano cartesiano.
c) Calcular la distancia entre dos puntos del plano
d) Determinar el punto medio entre dos puntos del plano.
En el curso de Matemática Básica se estudiaron los números reales y su representación en la recta numérica, después se continuó con el álgebra en una indeterminada o variable, es decir el estudio se concretó a la primera dimensión. Ahora, en esta unidad, los temas a tratarse se referirán a la segunda dimensión: el plano. Se estudiarán las relaciones y ecuaciones en dos variables con sus gráficas en el plano. El tema de mayor relevancia serán las funciones. Palabra ésta de mucho uso en nuestro lenguaje familiar, porque siempre estamos relacionando causa y efecto. Por ejemplo, nuestras calificaciones dependen de la dedicación al estudio, nuestro peso de la cantidad de alimentos que comamos, etc.
Para poder realizar estos estudios se necesitan conocimientos previos y básicos, de manera que comenzaremos con definiciones, como sistema de ejes coordenados, pareja ordenada,.
Los números ordenados x, y, que componen la pareja (x,y), son llamados las coordenadas del punto P representado en el plano; se denota por P(x, y), y se lee "el punto P de coordenadas x, y". Además, al valor de x, primera componente de la pareja, se le llama la abscisa de P, y al valor de y, segunda componente de la pareja, se le llama la ordenada de P.
Además, toda pareja ordenada de números reales representa un punto en el plano, y todo punto del plano se nombra o denota por medio de una pareja ordenada de números reales o coorde-nadas del punto. Hay una correspondencia uno a uno entre parejas y puntos del plano.
1.2 RELACIONES.
Objetivos
a) Definir una relación.
b) Determinar el dominio y rango o contradominio de una relación.
c) Calcular la relación inversa de una relación dada.
En nuestra vida cotidiana son frecuentes las relaciones de todo tipo: "madre-hijo", "profesor-alumno", "empleado-jefe", "paciente-médico", etc. En matemática, esta palabra "relación" es usada en forma semejante pero es preciso indicar el nexo entre los dos elementos como en: "a -igual- b", "x -menor que- y", "v -doble de- u" que se escribe simbólicamente por:
"a = b", "x < y" "v = 2u".
Cada una de esas "relaciones" tiene varias parejas de números que las verifican, cumplen o satisfacen la expresión, como por ejemplo:
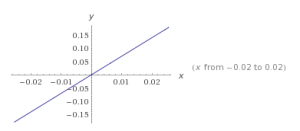
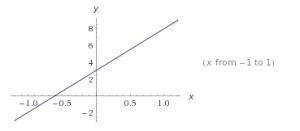
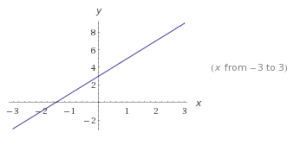
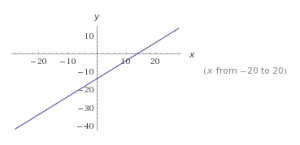
Para a = b se tienen (3, 3), (-2, - 2), (- 2/3, - 2/3), (π,π), (0.02, 0.02), ...
Para x < y se tienen (2, 5), (- 3, 0), (2, π), (-24, - 8), (0.3, 0.31), ...
Para v = 2u se tienen (1, 2), (3, 23), (0.001, 0.002), (- 2, -1), (-π, - 2π), ...
Relación: Todo subconjunto S de ℜ5 es una relación en los números realesℜ. Dos relaciones son iguales si tienen los mismos elementos.
Dominio y Rango de una relación: Se llama dominio de una relación al conjunto de las primeras componentes de las parejas de la relación; y se llama rango o contradominio de una relación al conjunto de las segundas componentes de sus parejas.
Ejemplo 3. Halle el dominio y rango para la relación {(x, y)∈ ℜ5| y =1/x+3}
Solución: En la ecuación de la relación dada, la variable x puede sustituirse por cualquier valor real, excepto x = -3, porque se anula el denominador y no es posible dividir entre 0.
Luego, su dominio es D = { x 0 | x … - 3 }. ℜ
Para saber el rango o contradominio, hay que buscar los valores prohibidos para y, y eso se consigue despejando x en función de y, así
Si y =1/x+3 entonces x =1-3y/y− en donde y es distinto de 0, por consiguiente,
el rango es R = { y 0 ℜ | y … 0 }
En general, para determinar el dominio y el rango de una relación dada por una ecuación, se escribe la ecuación en forma explícita para cada variable y se excluyen los valores prohibidos (ceros del denominador, números negativos bajo un radical par). El dominio es un subconjunto del Eje X y el rango un subconjunto del Eje Y, o sean subconjuntos de los números reales. Dos relaciones iguales tienen el mismo dominio y el mismo rango.
Inversa de una pareja ordenada y Relación Inversa: La inversa de una pareja ordenada de números se obtiene cambiando su orden: la primera componente pasa a ser segunda componente y la segunda componente al lugar de la primera. La inversa de la pareja (x, y) es (y,x). Una relación inversa se obtiene cambiando el orden de todas sus parejas, esto es invirtiendo todos sus elementos.
Observe que dominio y rango de la relación directa se intercambian para la relación inversa.
II. Ecuación de la Recta.
Por experiencia sabemos que dos puntos determinan el segmento de recta por el que pasa una recta, y que esa recta es única. En el plano cartesiano, una ecuación con dos variables de primer grado tiene como gráfica una recta, así 2x – 5 = 3y grafica como una recta. La fórmula normal de la recta es Ax + By + C = 0, escrita en forma implícita, o bien y = mx + b en forma explícita.
A la fórmula normal Ax + By + C = 0, en las dos variables x, y, y con coeficientes numéricos A y B y constante C, corresponde como gráfica una recta en el plano cartesiano, y a toda recta del plano cartesiano le corresponde una ecuación como la fórmula escrita.
Por ejemplo, las ecuaciones 7x – 3y – 5 = 0, o x - ½y = 7/4 tienen como representación gráfica sendas rectas en el plano cartesiano.
Para trazar una recta, lo más práctico es buscar sus puntos de intersección con los ejes X e Y.
Conocida la ecuación, los puntos de intersección se calculan dando el valor de cero a cada una de las variables, así: el punto de intersección con el
a) Eje X se obtiene cuando y = 0, y se denota por I(x1, 0) x
b) Eje Y se obtiene cuando x = 0, y se denota por I(0, y1). y
En la gráfica del ejemplo anterior, los puntos de intersección son I(5/2, 0) y I(0, - 5/3). xy
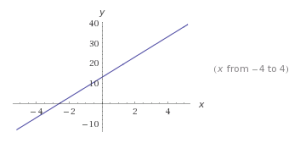
Otra fórmula normal de la ecuación de una recta es y = mx + b, escrita en forma explícita (la variable y aparece aislada). En esta forma, y = mx + b, el valor de m destaca la característica inclinación de la recta respecto al eje X orientado a la derecha, llamada pendiente de la recta, y el valor de b indica el corte en el eje Y, o sea I(0, b). y
Ambas fórmulas: Ax + By + C = 0, y = mx + b representan rectas en el plano. Y toda ecuación de una recta puede escribirse en una o en ambas formas.
Ejemplo de ecuaciones equivalentes:

Buenos Días Jóvenes Estudiantes de la Facultad de Ciencias Económicas de la UNAH.
Queremos motivar la Participación en la Clase de Métodos Cuantitativos II, de la Sección 1800, y cualquier otra Sección, con el propósito de darle un vuelco de 180 Grados a la problemática de comprensión del Álgebra y las aplicaciones al campo de la Administración, y la Economía .
A lo largo de los años hemos descubierto la debilidad en el área de Matemáticas, cuando ingresan a nuestra Facultad, muchas veces por la falta de cobertura del Currículo adecuado en la Materia, otras veces por el bajo nivel de quienes les instruyeron anteriormente y seamos sinceros, otras veces por la actitud del estudiante, en fin es la suma de todos esos factores y otros, que nos lleva a obtener resultados nada halagadores.
Intentaremos vencer esos obstáculos con apenas un propósito, cambiar " La Actitud de Estudio", y sera a partir de allí que haremos la diferencia, este Blog, pretende eso, así, que a estudiar todos, busquemos nuestro rincón favorito o el que tengamos, compre monos una resma de papel Bond, un Lápiz carbón y borrador ah y un cesto de basura para tirar lo que nos salga mal. Repasemos ese camino juntos, al final celebraremos frutos de ello.
Iniciamos por ahora con el contenido del Segundo Parcial, repasemos el contenido:
Por ahorita, nos quedamos aquí.
Queremos motivar la Participación en la Clase de Métodos Cuantitativos II, de la Sección 1800, y cualquier otra Sección, con el propósito de darle un vuelco de 180 Grados a la problemática de comprensión del Álgebra y las aplicaciones al campo de la Administración, y la Economía .
A lo largo de los años hemos descubierto la debilidad en el área de Matemáticas, cuando ingresan a nuestra Facultad, muchas veces por la falta de cobertura del Currículo adecuado en la Materia, otras veces por el bajo nivel de quienes les instruyeron anteriormente y seamos sinceros, otras veces por la actitud del estudiante, en fin es la suma de todos esos factores y otros, que nos lleva a obtener resultados nada halagadores.
Intentaremos vencer esos obstáculos con apenas un propósito, cambiar " La Actitud de Estudio", y sera a partir de allí que haremos la diferencia, este Blog, pretende eso, así, que a estudiar todos, busquemos nuestro rincón favorito o el que tengamos, compre monos una resma de papel Bond, un Lápiz carbón y borrador ah y un cesto de basura para tirar lo que nos salga mal. Repasemos ese camino juntos, al final celebraremos frutos de ello.
Iniciamos por ahora con el contenido del Segundo Parcial, repasemos el contenido:
- Funciones: El Plano Cartesiano, el Par Ordenado, Teoría de Funciones, Regla de Correspondencia, Relaciones, diferencia entre relación y función.
- Funciones Discretas: Tipo de Funciones, Gráfica el Plano cartesiano, Dominio, Rango
- Funciones Lineales: Pendiente, Creciente, Decreciente, Nula, Inexistencia de Pendiente, Forma Ordenada punto al Origen, Forma ordenada Punto Pendiente,
- Gráfica de Funciones Lineales, a partir de dos puntos, Intercepciones en el eje de las abscisas y las Ordenadas Tabla de Valores Ix (x,0) y Iy(0,y).
- Aplicaciones de la Función Lineal, Costo Lineal, el Ingreso, el Costo fijo y el costo Variable, la Utilidad, la Oferta y la Demanda.
- la Función de Grado dos ( Cuadrática), su gráfica (la Parábola), el procedimiento para graficar, sus aplicaciones, Ingreso y Utilidad Máxima, el costo Mínimo.
- La Función Valor Absoluto, su procedimiento para Graficar
- La Función Raíz Cuadrada
- La función Racional.
Por ahorita, nos quedamos aquí.
Suscribirse a:
Entradas (Atom)